Understanding Variance, Covariance, and Correlation
What is Variance? One possible answer is \(\sigma^2\), but this is just a mechanical calculation (and leads to the next obvious question: what is \(\sigma\)?). Another answer might be the "the measure of the width of a distribution", which is a pretty reasonable explanation for distributions like the Normal distribution. What about multi-modal distributions, distributions having not just one peak but many and of different widths? Following this we might want to say "How much a Random Variable varies?" but now we're getting back to where we started!
Variance - squaring Expectations to measure change
In mathematically rigorous treatments of probability we find a formal definition that is very enlightening. The variance of a random variable \(X\) is defined as:
$$Var(X) = E(X^2) - E(X)^2$$
Which is so simple and elegant that at first it might not even be clear what's happening. In plain English this equation is saying:
Variance is the difference between when we square the inputs to Expectation and when we square the Expectation itself.
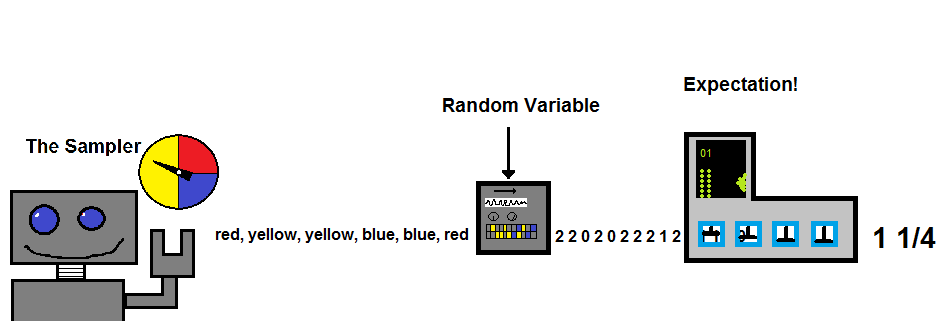
I'm guessing this may still not be entirely clear so we're going to bring back the robots and machines from our previous post on Random Variables and Expectation to help explain what this definition of Variance is saying. In the last post we ended up with this visualization of creating Expectation from a Sampler and a Random Variable.
Sampling Robot and the Expectation of a Random Variable.
Our Sampler spins a spinner (or flips a coin) and samples from the event space. These events are sent to a Random Variable which transforms events into numbers so we can do math with them. The numbers are then sent to the Expectation Machine which squashes all those numbers into a single value summarizing the output from the Random Variable. For Variance we just need one more, very simple, machine.
In it's most general form Variance is the effect of squaring Expectation in different ways.
This is the Squaring Machine, it just squares the values passed into it. Because squaring is a non-linear function where we place it in our mathematical assembly line will lead to different results. We're going to re-use our spinning robot from the post on Random Variables, which outputs yellow, red and blue with the following probabilities:
$$P(\text{yellow}) = 1/2, P(\text{red}) = 1/4, P(\text{blue}) = 1/4$$
and our Random Variable will be \(A\) defined as:
Now we can create two nearly identical setups of machines, only we'll change the location of the the Squaring Machine.
Variance is the difference of squaring out Random Variable at different points when we calculate Expectation.
Squaring before calculating Expectation and after calculating Expectation yield very different results! The difference between these results is the Variance. What is really interesting is the only time these answers are the same is if the Sampler only outputs the same value each time, which of course intuitively corresponds to the idea of there being no Variance. The greater the actual variation in the values coming from the Random Variable is the greater the different between the two values used to calculate Variance will be. At this point we have a very strong, and very general sense of how we can measure Variance that doesn't rely on any assumptions our intuition may have about the behavior of the Random Variable.
Covariance - measuring the Variance between two variables
Mathematically squaring something and multiplying something by itself are the same. Because of this we can rewrite our Variance equation as:$$E(XX) - E(X)E(X)$$This version of the Variance equation would have been much messier to illustrate even though it means the same thing. But now we can ask the question "What if one of the Xs where another Random Variable?", so that we would have: $$E(XY) - E(X)E(Y)$$
And that, simpler than any drawing could express, is the definition of Covariance (\(Cov(X,Y)\)). If Variance is a measure of how a Random Variable varies with itself then Covariance is the measure of how one variable varies with another.
Correlation - normalizing the Covariance
Covariance is a great tool for describing the variance between two Random Variables. But this new measure we have come up with is only really useful when talking about these variables in isolation. Imagine we define 3 different Random Variables on a coin toss:
Now visualize that each of these are attached to the same Sampler, such that each is receiving the same event at the same point in the process.
Correlation between different Random Variables produce by the same event sequence
The only real difference between the 3 Random Variables is just a constant multiplied against their output, but we get very different Covariance between any pairs.
$$Cov(A,B)=2.5,Cov(A,C)=25,Cov(B,C)=250$$
Our Covariance function doesn't have enough information to tell us that effectively \(A\),\(B\), and \(C\) are the same. The problem is that we are no longer accounting for the Variance of each individual Random Variable. The way we can solve this is to add a normalizing term that takes this into account. We'll end up using
$$\sqrt{Var(X)\cdot Var(Y)}$$
The property we've been trying to describe is the way each of these Random Variables correlate with one another. Putting everything we've found together we arrive at the definition of Correlation:
$$Corr(X,Y) = \frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}}$$
But wait a second, where does $$\sqrt{Var(X)\cdot Var(Y)}$$ come from? The short answer is The Cauchy-Schwarz inequality . Exploring the relationship between Correlation and the Cauchy-Schwarz inequality deserves its own post to really develop the intuition. For now it is only important to realize that dividing Covariance by the square root of the product of the variance of both Random Variables will always leave us with values ranging from -1 to 1.
Conclusion - tying these measurements together
We have now covered Random Variables, Expectation, Variance, Covariance, and Correlation. These are basic components of probability and statistics. Despite this they tend to be often poorly understood. I hope this post and the last have shown how they are all elegantly relate to one another:
A Random Variable, \(X\) , is a set of numeric outcomes assigned to probablistic events.
Expectation,\(E(X)\) , is the outcomes of a Random Variable weighted by their probability.
Variance is the difference between Expectation of a squared Random Variable and the Expectation of that Random Variable squared: \(E(XX) - E(X)E(X)\).
Covariance, \(E(XY) - E(X)E(Y)\) is the same as Variance, only two Random Variables are compared, rather than a single Random Variable against itself.
Correlation, \(\frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}}\), is just the Covariance normalized.
If you want to dive even deeper into the why of Variance as well other other ways of summarizing a Random Variable checkout out this post on Moments of a Random Variable.
Want to learn about Bayesian Statistics and probability? Order your copy of Bayesian Statistics the Fun Way No Starch Press!
If you also like programming languages, you might enjoy my book Get Programming With Haskell from Manning.