Popular Posts
Confused by Hypothesis tesing used in A/B Tests? In this post we take a look at building an A/B from scratch the Bayesian way!
Monte Carlo simulations are very fun to write and can be incredibly useful for solving ticky math problems. In this post we explore how to write six very useful Monte Carlo simulations in R to get you thinking about how to use them on your own.
There is an iconic probability problem in The Empire Strikes Back! Han Solo is told that navigating an asteroid field is extremely unlikely to be successful. However not only does he navigate the asteroid field successfully, but we know he will. Learn how we can use Bayesian Priors to reconcile C3POs frequentist views on probability with our natural reasoning.
Find Bayes' Theorem confusing? Let's break down this famous formula using Lego to help you build up a better intuition for this foundational concept!
All Posts
In this post we walk through the architecture of diffusion models and show how to build one using only linear models as components!
In this post we see if GPT is powerful enough to be able to accurately predict the winner of a headline A/B test! Along the way we explore multiple approaches an modeling languages and learn how to build a model that can predict the difference between two vectors.
In this post we take a look a how the mathematical idea of a convolution is used in probability. In probability a convolution is a way to add two random variables. Using a slightly ridiculous, mad-science, example we walk through multiple way to compute a convolution and ultimate arrive at the formula with a better understanding of this powerful concept!
In this post we explore how we can use the Black-Scholes Merton model, together with the volatility smile of real options prices to determine the probability that Elon Musk will successfully purchase Twitter.
In this post we explore using censored data for an estimation problem. Our example is 100 scientist asked if they believe the weather at a time in the future will be lower or higher than specified number. We end up with a continuous distribution representing the beliefs of the scientists.
In this post we take a deep dive exploring the topic of Modern Portfolio Theory. We slowly walk through modeling a single stock, multiple correlated stocks and finally optimizing our portfolio. We’ll be making use of JAX to build our model with allows for easy optimization with the techniques of differentiable programming.
In this post we use Bayesian reasoning to understand the media, specifically an article about politically motivated interstate moving in the US as written about by NPR. We see that an important part of Bayesian reasoning is that our beliefs are never fixed.
In this post we use statistics and historic weather data to help answer the question “is it really getting warming in December in NJ?” Using progressively more complex linear models we find some surprising results about what’s happening to weather in the area.
In this post we explore the very curious logit-normal distribution, which appears frequently in statistics and yet has no analytical solutions to any of its moments. We end with a discussion of Nietzsche and what Dionysian statistics might mean. It’s a bit of an odd post that’s for sure.
Exploring how Frequentist and Bayesian methods differ when looking at the common problem of predicting misfires in extra-dimensional alien technologies. We explore the nice property that Bayesian statistics are mathematically correct and then consider that sometimes being “technical wrong” does work out.
In part 2 of our series exploring the relationship between Inference and Prediction we explore modeling Click Through Rate as a Statistical modeling problem so that we can more deeply understand the role of Inference in modeling.
This post is the first in a three part series covering the difference between prediction and inference in modeling data. Through this process we will also explore the differences between Machine Learning and Statistics. We start here with statistics, ultimately working towards a synthesis of these two approaches to modeling
Survivorship bias is a very common topic when discussing statistics and data science, but identifying survivorship bias is much easier than modeling it! In this post we take a look at modeling survivorship bias in MLS house listing using mathematics, Python and JAX and see just how challenging of a task it is.
Thompson sampling is a technique to solve multi-armed bandit problems but choosing actions based on the probability they offer the highest expected reward. In this post we learn about this technique by implementing an ad auction!
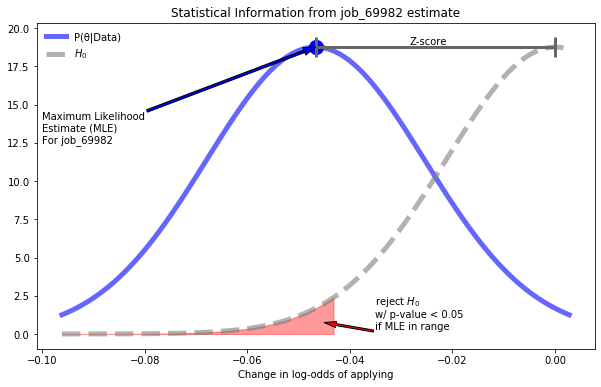
Bayesian statistics rely heavily on Monte-Carlo methods. A common question that arises is “isn’t there an easier, analytical solution?” This post explores a bit more why this is by breaking down the analysis of a Bayesian A/B test and showing how tricky the analytical path is and exploring more of the mathematical logic of even trivial MC methods.
This is a very different post than the usual for this blog, but for this very reason it is important. I write about one of the paper’s that has had the biggest influence on me: Audre Lorde’s “The Master’s Tools Will Never Dismantle the Master’s House”.
Video and lecture notes from a tutorial on Probability and Statistics given at PyData NYC 2019. This tutorial provides a crash course in probability in statistics that will cover the essentials including probability theory, parameter estimation, hypothesis testing and using the generalized linear model all in just 90 minutes!
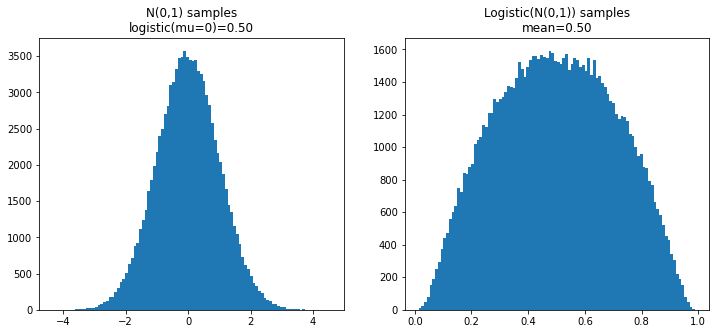
When you train a logistic model it learns the prior probability of the target class from the ratio of positive to negative examples in the training data. If the real world prior is not the same as your training data, this can lead to unexpected predictions from your model. Read this post to learn how to correct this even after the model has been trained!
In this post we’ll explore how we can derive logistic regression from Bayes’ Theorem. Starting with Bayes’ Theorem we’ll work our way to computing the log odds of our problem and the arrive at the inverse logit function. After reading this post you’ll have a much stronger intuition for how logistic regression works!
In this post we're going to take a deeper look at Mean Squared Error. Despite the relatively simple nature of this metric, it contains a surprising amount of insight into modeling.
Kullback–Leibler divergence is a very useful way to measure the difference between two probability distributions. In this post we'll go over a simple example to help you better grasp this interesting tool from information theory.
A guide for getting started with Bayesian Statistics! Start your way with Bayes' Theorem and end up building your own Bayesian Hypothesis test!
Bayesian Reasoning with the Mystic Seer: Bayes' Factor, Prior Probabilities and Psychic Powers!
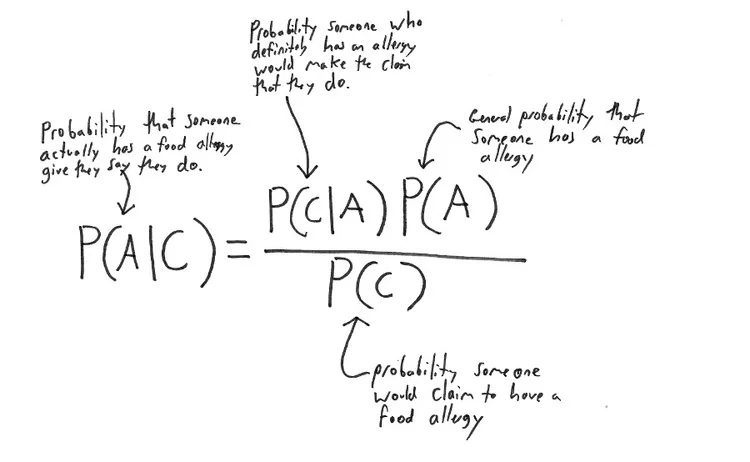
Your friends probably don't have a food allergy, but how sure are you?
How likely is it that your friends really have food allergies? More important should you believe them? In this post we look at using Bayes' theorem to model this everyday question.
Use Markov Chains and Linear Algebra to solve this holiday puzzle!
In this post we look at the classic Coupon Collector's problem as well as a more interesting variant of it!
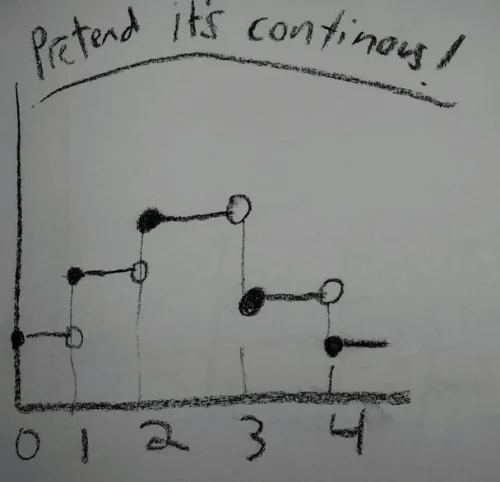
Part 2 in our exploration of the Lebesgue Integral
In this post we use a strange tea party to explore a practical understanding of the Lebesgue integral
Using pictures to explain the idea of Probability Spaces in Rigorous Probability Theory
In this post we discuss an intuitive, high level view of measure theory and why it is important to the study of rigorous probability.






























Use Markov Chains and Linear Algebra to solve this holiday puzzle!