This post has been updated and rewritten as a chapter in my book Bayesian Statistics the Fun Way!

In the last post we looked at how we could estimate the conversion rate for visitors that subscribe to my email list. In order to understand how the Beta distribution changes as we gain information let's look at another conversion rate. This time we'll look at email subscribers and try to figure out how likely they are to click on the link to a post given that they open the email I sent them. I use MailChimp which gives you real-time info about how many people who have opened an email have clicked the link to your post. This both great and horrible since the data is helpful, but easy to excessively obsess over!

Modeling our data

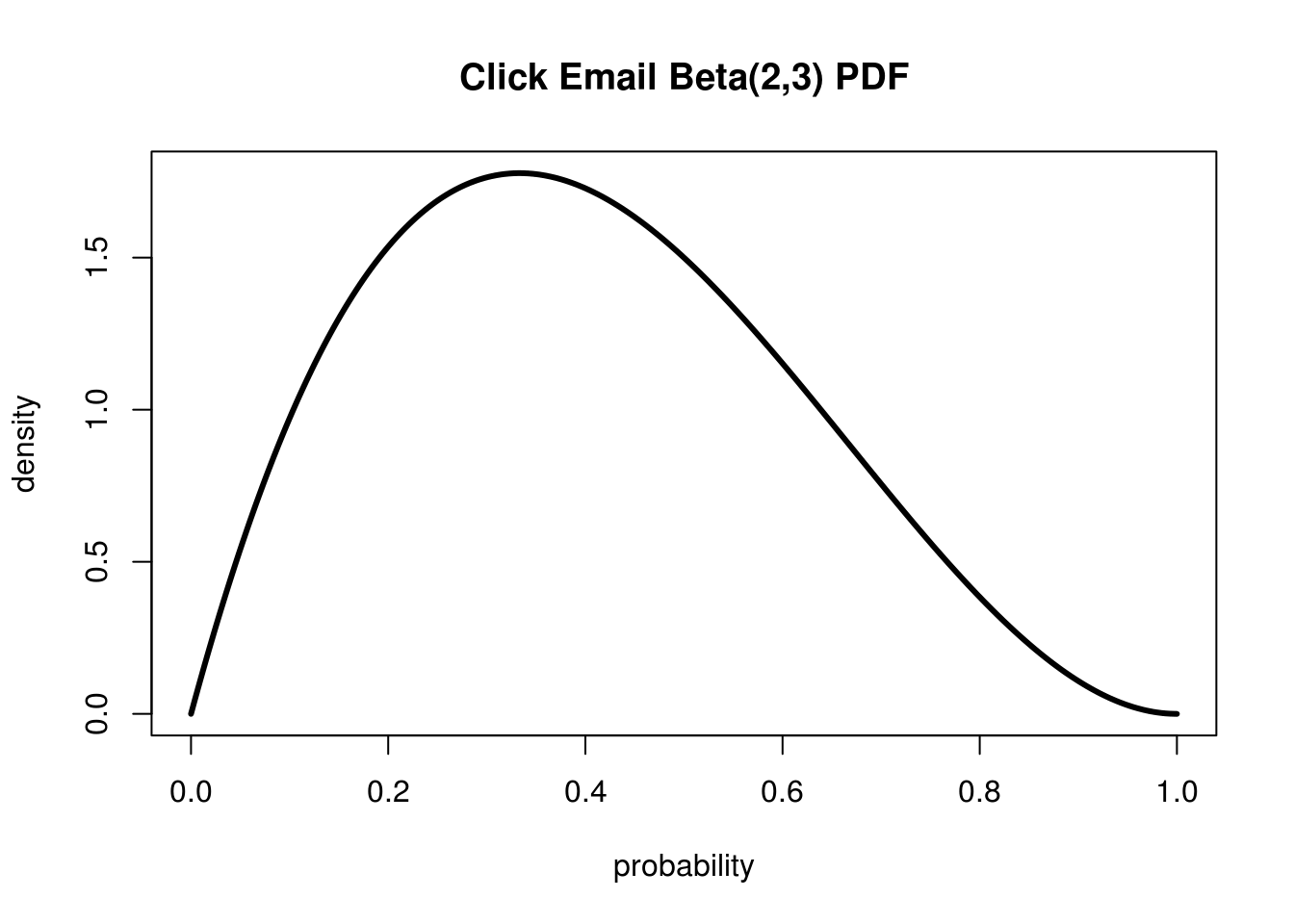
Let's say that out of the first 5 people that open an email 2 of them click. This is our Beta distribution corresponding to this data:

With a small sample, our Beta distribution covers a wide range of possibilities

Unlike our last post, where we had a pretty narrow spike, we have this huge range of possible values. Here's the CDF so that we can reason about these probabilities a little easier:

Using the CDF allows for easier estimation of interesting quantiles and confidence intervals

I've marked of the 95% confidence interval (ie 95% chance our true rate is somewhere in there) to make it easier to see. At this point our true conversion rate could be pretty much anything between 0.05 and 0.8! This reflects the very little information that we actually have acquired so far. Given that we have had 2 conversions we know the true rate can't be 0, and we also know that it can't be 1 since we've had 3 people not convert. Everything else is pretty much fair game.

Estimating with a Prior Probability

But wait a second, I'm pretty new to this email list game but 80% click-through? That sounds pretty unlikely. I subscribe to plenty of email lists, but I definitely don't click through to the content 80% of the time that I open the email. Maybe I'm an outlier, but saying that 80% is a credible value seems pretty suspicious to me. It turns out MailChimp thinks so too. I list my blog as "Education and Training" and MailChimp claims that on average only 2.4% people who open emails in that industry click through to the content.

If you are a frequent reader of this blog you'll be familiar with this problem from the post on Han Solo and Bayesian Priors. Our data tells us one thing, but our background information tells us another. In Bayesian terms, the data we have observed is our Likelihood and the information from our personal experience and MailChimp is our Prior Probability. Our challenge now is that we have to figure out how to model our prior. Luckily, unlike the case with Han Solo, we actually have a some data here to help us.

Using Data to Establish our Prior

MailChimp says the conversion rate for most people in the same space as this blog is 2.4%. This give us a starting place, but there are still several different Beta distributions we could use to model this: Beta(1,41) Beta(2,80), Beta(5,200),Beta(24,976), etc. So which should we use? Let's plot some of these out and see what they look like:

Different Beta distributions can be used to represent different strengths of belief in the same data.

As we can see the lower the combined $\alpha + \beta$ the wider our distribution is. The problem is even the most liberal option we have, Beta(1,41), seems a little too pessimistic. But what do I know? Let's stick with this one since it is based on data.

Remember that we can calculate our Posterior Distribution (the combination of our Likelihood and our Prior) by simply adding together the two Beta distributions:

$$Beta(\alpha_\text{posterior},\beta_\text{posterior}) = Beta(\alpha_\text{likelihood} + \alpha_\text{prior}, \beta_\text{likelihood} + \beta_\text{prior})$$

Updating our beliefs with a Prior

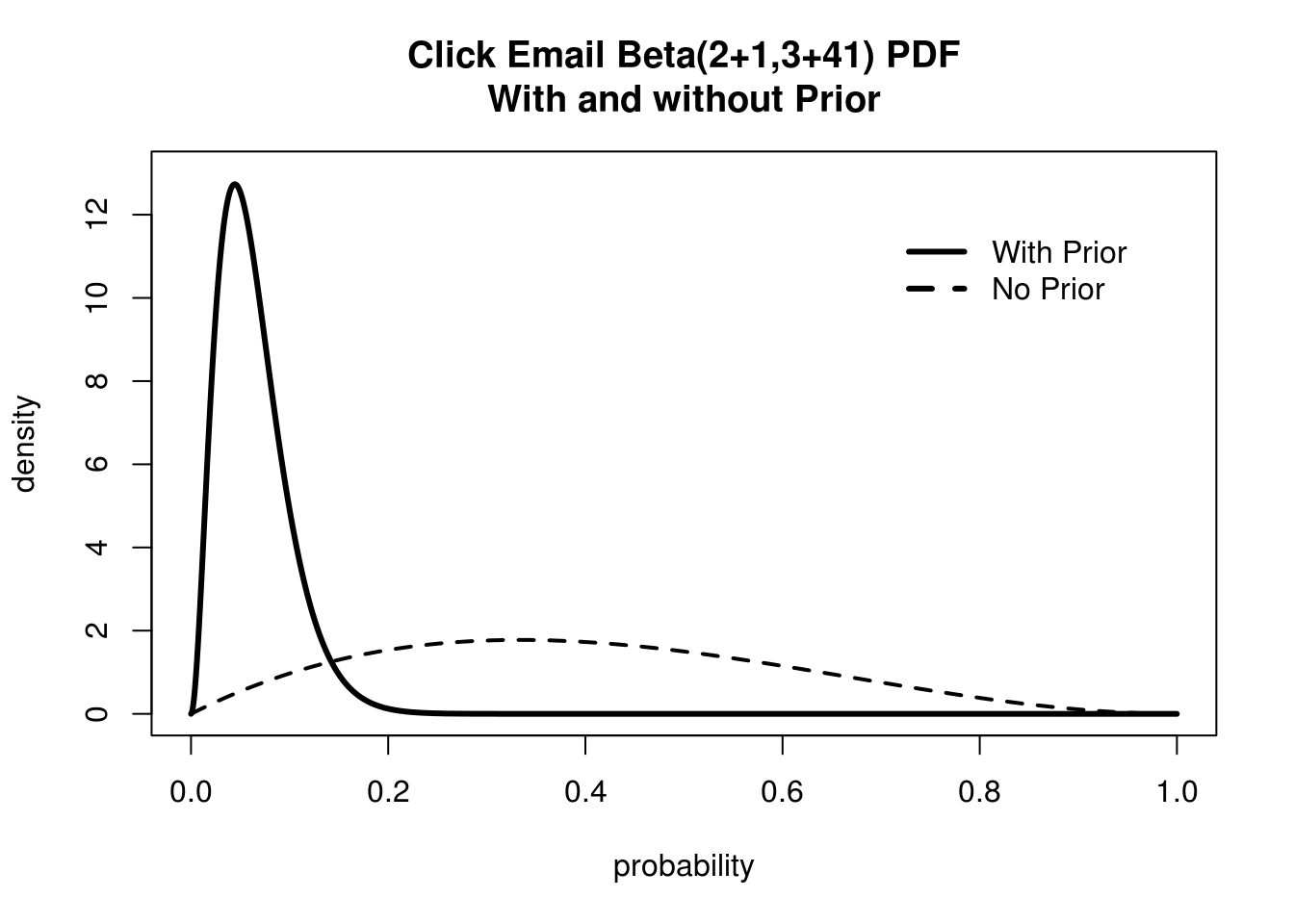
Now we can compare our beliefs with and without priors.

Adding a Prior Probability can drastically improve estimate from small sample sizes.

Wow! That's quite sobering. We can definitely throw out the chance that we have an 80% conversion rate. But I still think MailChimp is being pessimistic. How can we prove them wrong? We can do this the way any rational person does, with more data! We stop staring at MailChimp statistics for a few hours, and when we come back and we find that now we have 25 people out of 100 that have clicked! Let's look at how the difference between our Posterior and our Likelihood looks now:

The more data we collect the less our prior influences of final beliefs

This is quite an improvement! Our beliefs with and without Prior information look much more similar than before. Our Prior is still keeping our ego in check, giving a more conservative estimate for our true conversion rate. Here we can see that evidence is doing what it should, slowly swaying our beliefs to what the data suggests. Okay, let's wait overnight and come back!

In the morning we find 86 out of 300 people have clicked through! Here are our updated beliefs:

As we can see, more data means the eventual convergence of different priors

What we are witnessing is the most important thing to realize about Bayesian statistics: The more data we gather the more our Prior beliefs become diminished by evidence! When we had no evidence our Likelihood proposed some things we know are absurd. In light of little evidence, our Prior beliefs squashed any data we had. But as we continue to gather data that disagrees with our Prior our Posterior beliefs shift towards what the data tells us and away from what our initial thoughts were. Another important thing to realize is that we started with a pretty pessimistic prior. Even then after just a day of collecting a relatively small set of information we were able to find a Posterior that seems much, much more reasonable.

Learn more about Bayesian Statistics in my book Bayesian Statistics the Fun Way!

If you enjoyed this post please subscribe to keep up to date and follow @willkurt!