Parameter Estimation - The PDF, CDF and Quantile Function
This post is part of our Guide to Bayesian Statistics and an updated version is included in my new book Bayesian Statistics the Fun Way!
When we start learning probability we often are told the probability of an event and from there try to estimate the likelihood of various outcomes. In reality the inverse is much more common: we have data about the outcomes but don't really know what the true probability of the event is. Trying to figure out this missing parameter is referred to as Parameter Estimation.
For example suppose I want to know what the probability is that a visitor to this blog will subscribe to the email list (do it for science!). In marketing terms getting a user to perform a desired event is referred to as the conversion event or simply a conversion and the probability that a user will convert is the conversion rate. If you read the earlier post on Discrete and Continous Probability distributions you'll know that the way we can determine \(p\), the probability of subscribing given that we know \(k\), the number of people subscribed and \(n\) the total number of people who visited is to use the Beta distribution. There are two parameters for the Beta distribution, \(\alpha\) in this case representing the total subscribed (\(k\)), and \(\beta\) representing the total not subscribed (\(n-k\)).
The Probability Density Function
In this case, let's say for first 40,000 visitors I get 300 subscribers. That would be \(Beta(300,39700)\) (remember \(\beta\) is the number of people who did not subscribe, not the total). We can visualize the Probability Density Function (PDF) for this Beta Distribution as follows:
The Beta distribution is very useful for estimating unknown probabilities
What does this PDF represent? From our data we can infer that our average conversion rate is simply \(\frac{\text{subscribed}}{\text{visited}} = \frac{300}{40000}=0.0075\). Clearly it is unlikely that our conversion rate is exactly 0.0075 rather than say 0.00751. We can use the area under parts of this curve (which is simply the integral) to determine exactly how likely different probabilities for our true conversion rate are given the data we have seen. The area under the curve less than 0.0065 represents the possibility that we got very lucky with many of our observations and our conversion rate is actually much lower. We can use our PDF to compare two extremes. The probability that our conversion rate is actually much lower than we have seen is:$$P(\text{much lower}) = \int_{0}^{0.0065}Beta(300,39700) \approx 0.008$$
And we can ask the other question "how likely is it that we actually got unlucky and our true conversion rate is greater than 0.0085?":$$P(\text{much higher}) = \int_{0.0085}^{1}Beta(300,39700) \approx 0.012$$
This means that the probability that our conversion rate is much higher than we observed is actually a bit more likely that the probability that it is much less than observed!
Introducing the Cumulative Distribution Function!
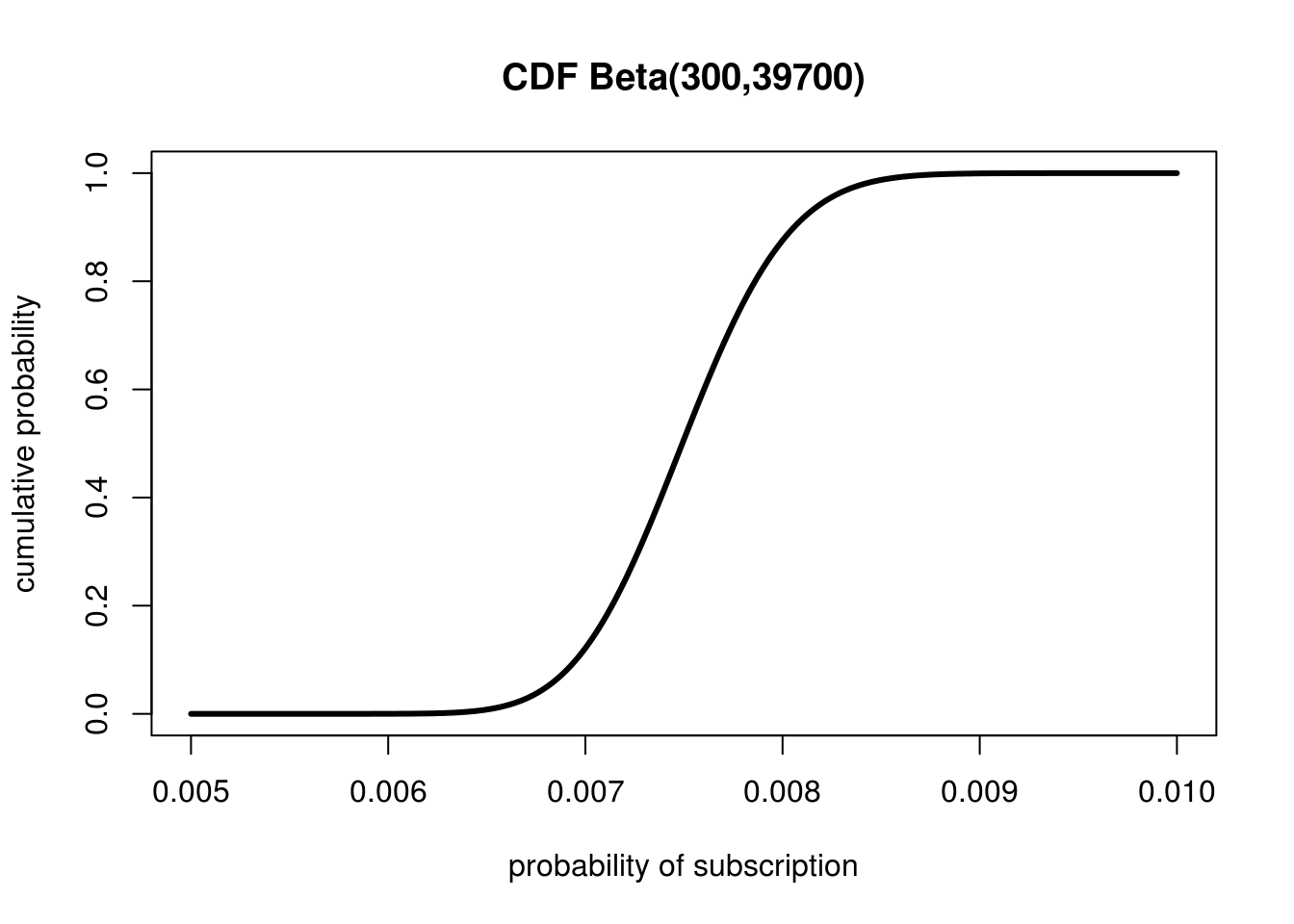
I know you're thinking: "I do so much love taking all these integrals each time I have different question!" But let's make the radical assumption that you'd prefer to just look at a plot and get these answers! Despite its ubiquity in probability and statistics, the PDF is actually a pretty mediocre way to look at data. The PDF is only really useful for quickly ascertaining where the peak of a distribution is and getting a rough sense of the width and shape (which give a visual understanding of Variance and Skewness). A much better (for more reasons than we'll cover here) function is the Cumulative Distribution Function (CDF). The CDF, for any probability distribution, tells how probable it is that a value is below \(x\) in our distribution. The CDF for our problem looks like this:
The Cumulative Distribution Function can be used to quickly estimate precentiles
The CDF is so simple it might seem useless, so let's go over a few visual examples of how we can use this amazing tool.
First we can easily see the median (which can even be challening to compute analytically) by visually drawing a line from the point where the cumulative probability is 0.5 (meaning 50% of the points are below this point and 50% are above). Looking where this intersects the x-axis give us our median!
The CDF allows for quick and accurate estimates of the median (and other quantiles!)
We can see that the median is very close to the Expectation of 0.0075.
If we just need an approximate value we also can save all that integral work we did before for assessing the probability of ranges of values. To estimage the probability that the conversion rate is between 0.0075 and 0.0085 we can trace lines from the x-axis at these points, then see where the meet up with the y-axis. The distance between them is the approximate integral.
Integration has never been so easy!
Eyeballing the CDF we can see that on the y-axis these values range from roughly 0.5 to 0.99, meaning that there is roughly a 49% chance that our true conversion rate lies somewhere between these two values. The best part is we didn't have to do any integration! But why does this trick work so easily? The answer is actually pretty awesome. It turns out that the PDF is simply the derivative of the CDF! Looking at it the other way: given a PDF when we visualize the CDF we're actually visualizing the anti-derivative which is the basis for how we calculate integrals in the first place. The reason we can perform visual integration is because we are, quite literally, visually integrating the PDF.
One final trick we can ask is about our Confidence Interval. Now that we know there is a range of possible values we could have, it is sensible to ask "What is the range that covers 80% of the possibilities?". We answer this question by combining our previous approaches. We start at the y-axis and draw lines from 0.1 and 0.9, and then simply see where on the x-axis these intersect with our CDF.
CDFs make estimating confidence intervals accuracy much easier than PDFs
As we can see the x-axis is interesected at roughly 0.007 and 0.008 which means that there's an 80% chance that our true conversion rate falls somewhere between these two values.
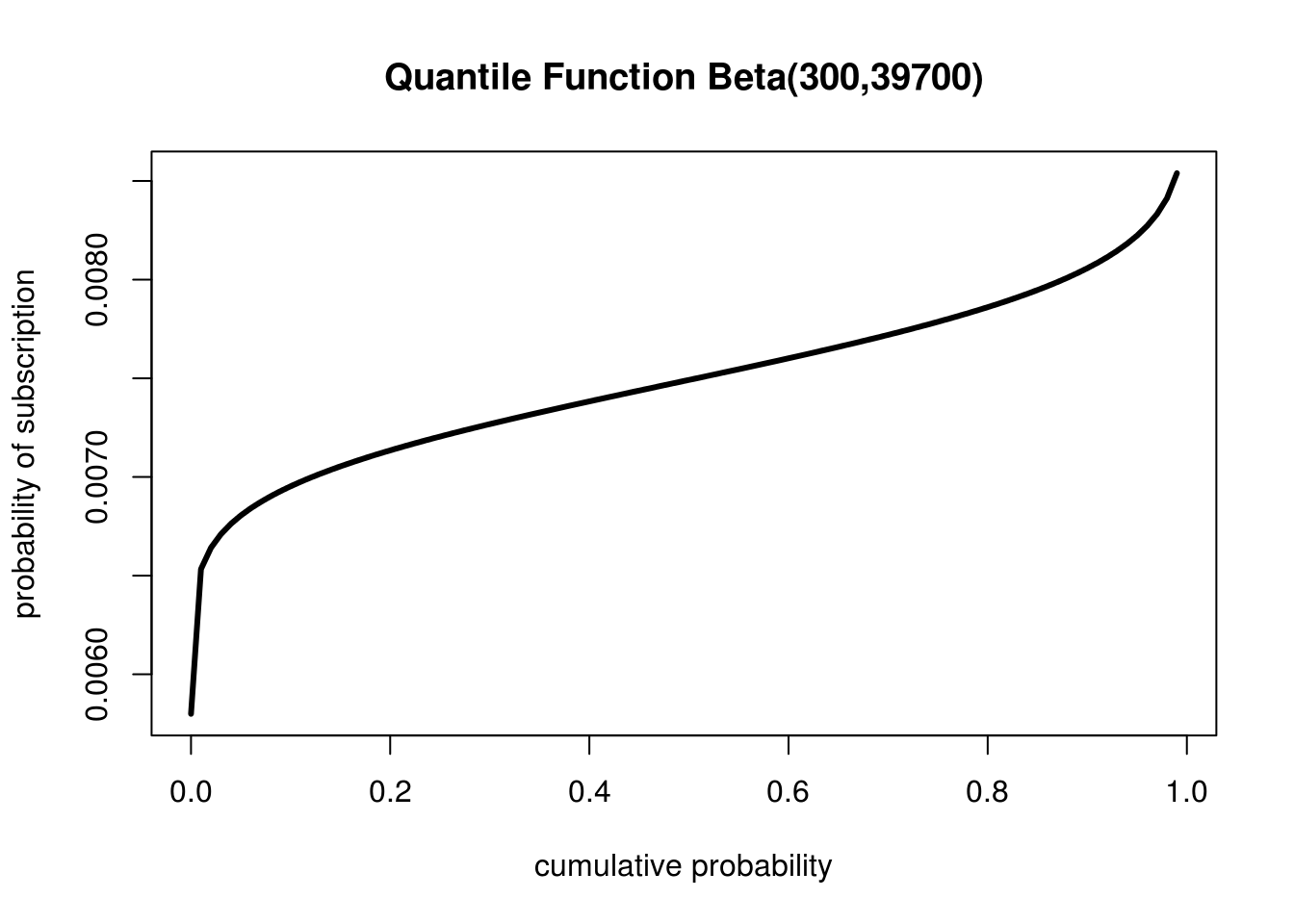
The Quantile Function
The careful reader might have noticed that we did something visually that is not necessarily as easy to do mathematically. For both the median and confidence interval examples we started with the y-axis and used that to find a point on the x-axis. However mathematically the CDF takes an \(x\) and gives us \(f(x) = y\), but in these cases we are actually estimating \(f(y) = x\). What we have done visually is to compute the inverse of the CDF. The inverse of the CDF is an incredibly common and useful tool called the Quantile Function. As we can see, visually the Quantile Function is just the CDF rotated:
Simply turn your CDF sideways and you get the Quantile function
Since it is visually identical, ignoring rotation, to the CDF, visualizations of the Quantile Function are much less common. It is still an important tool to know since for actually computing both the median and the confidence interval you're going to need it.
Conclusion
We've covered a lot of ground and touched on the really interesting relationship between the Probability Density Function, Cumulative Distribution Function, and the Quantile Function. However, there are many questions still remaining regarding our parameter estimation problem, which we will continue to explore in the next post.
The entire contents of this post received an updated (along with a bunch of great beginner material) in my book Bayesian Statistics the Fun Way!
If you enjoyed this post please subscribe to keep up to date and follow @willkurt!