Logistic Regression from Bayes' Theorem
In this post we'll take a helpful look at the relationship between Bayes' Theroem and logistic regression. Despite being a very commonly used tool in statistics, machine learning and data science, I've found people frequently get confused about the details of how logistic regression actually works. By showing you how you can derive logistic regression from Bayes' theorem you should have a much easier time remembering exactly how this useful tool works. Ultimately we'll see that logistic regression is a way that we can learn the prior and likelihood in Bayes' theorem from our data. This will be the first in a series of posts that take a deeper look at logistic regression.
The key parts of this post are going to use some very familiar and relatively straightforward mathematical tools. We're going to use to Bayes’ theorem
$$P(H|D) = \frac{P(D|H)P(H)}{P(D)}$$
which you can refresh in this post on Bayes’ Theorem with Lego, and the basic linear model
$$y = \beta x + \beta_0$$
Which just says that some target variable \(y\) can be understood as a linear combination of \(x\) multiplied by coefficients \(\beta\) plus some constant \(\beta_0\).
Logistic Regression Basics
As a quick refresher, logistic regression is a common method of using data to predict the probability of some hypothesis. More mathematically speaking we have some input \(x\), this could single value like someone's height or it could be an vector like the pixels in the image, and some \(y\) which represents an out come such as "can slam dunk a basketball" or "is picture of a cat". Our goal in logistic regression is to learn the probability of \(y\) given \(x\), or \(p(y|x)\). The model is trained on examples were \(y\) is a binary outcome, 1 meaning success and 0 being failure, and \(x\) is an example corresponding of data that resulted in the outcome \(y\). When we train the model we have a vector of \(y\) and a matrix \(X\), the rows of which represent training examples and the columns features.
Logistic regression is often described as an s-shaped function that squishes values to 0 or 1
So far so good, but here's where things usually get a bit confusing. In most treatments of this topic that I've seen, you're immediately shown this beautiful equation which is how we compute the probability of \(y\) given our \(x\):
$$p(y|x) = \frac{1}{1+e^{-(\beta_0 + \beta_1x)}}$$
This is the inverse logit, or the logistic, function. The \(\beta_0\) and \(\beta\) are parameters that we'll learn during training. The output has this familiar S-Shape seen in the graph on this page.
The intuition behind this is often explained as the logistic function forcing very large positive numbers to be close to 1 and very large negative numbers to be close to 0, which is ultimately what we want probabilities to look like. This is an okay explanation, but it misses the truly beautiful (and useful!) connection between logistic regression and Bayes' theorem.
Making a good cup of coffee
As a lifelong caffeine addict I will drink pretty much any cup of coffee if the situation demands, but I really love a good cup of coffee. My preferred style of making coffee is with a pour-over and a few months ago I decided that I really wanted to make consistently excellent coffee. To do this I began experimenting with different amounts of coffee, different volumes of water, etc. Let's think how we would model the perfect cup probabilistically.
Making a good cup of coffee requires a surprising amount of data!
First we want to represent our data. Even if we assume that we use the same beans, there are a lot of factors that go into the quality of brewing:
age of the beans
coarseness of the grind
weight of the grounds
duration of the pour
temperature of the water
And of course we could probably come up with even more things. We're not going to worry about actual data in this post, just how we would model this problem probabilistically.
Bayesian Brewing
Let's consider all of the possible things that I could account for in making a cup as our vector of data \(D\). And we want to know the probability of our hypothesis \(H\) which is "a great cup of coffee". Now we just want to answer the question, "given my set up for brewing what is the chance I get a great cup of coffee?". That is, we want to know \(P(H|D)\). Whenever we want to know the probability of a hypothesis given our data we can turn to Bayes' theorem!
$$P(H|D) = \frac{P(D|H)P(H)}{P(D)}$$
Let's refresh on the Bayesian terms for each part of this equation and what they mean.
\(P(H|D)\) is our posterior probability that we make a great cup of coffee given our setup
\(P(D|H)\) is our likelihood in having these setup we did given we made a good cup of coffee (this is a bit odd so we'll chat about this)
\(P(H)\) is our prior probability in making a good cup of coffee.
\(P(D)\) just normalized everything so our probability is appropriately scaled between 0 and 1 (we'll have a bit of an issue with this)
Before we go much further we have a few things we need to work out. Our prior probability, \(P(H)\) isn't too confusing, it's just generally the prior belief that we'll get a great cup of coffee out of our brew. Maybe half the cups we make are great, maybe only 1 in 100, but either way that's what this is representing.
The likelihood is a bit tricky to think about because we want to know that "Given I had a good cup of coffee, how likely is it I had this set up". That's a weird way to think about our problem. But that's exactly why we want to use "machine learning" here. We are going to come up with a simple model for this likelihood, which we'll discuss soon, so that we can learn this likelihood from data (we'll also be learning the prior as well).
That leaves only \(P(D)\) left, which is the probability of our data. But what is the probability of "this set up for brewing coffee"? Surely there are virtually infinite possibilities for the set up, so this is a problem. We can't solve for our posterior probability if we can't figure this out.
Comparing hypotheses using posterior odds
We need to deal with the fact that we really don't know \(P(D)\), but there's an easy fix for this if we just reframe our problem a bit. Right now we're only thinking about one hypothesis, that our cup of coffee is great, but there's obviously an alternative to this. If we consider \(\bar{H}\), which is simply the belief that our coffee is not great, we can compare our posteriors and look at our problem with out needing \(P(D)\). Now we also have \(P(\bar{H}|D)\), and we'll look at the ratio of this with \(P(H|D)\).
$$\frac{P(H|D)}{P(\bar{H}|D)} = \frac{P(D|H)P(H)\frac{1}{P(D)}}{P(D|\bar{H})P(\bar{H})\frac{1}{P(D)}}$$
Of course the \(\frac{1}{P(D)}\) appears in both the numerator and denominator so we can get rid of it. This means we no longer have to worry about \(P(D)\)!
$$\frac{P(H|D)}{P(\bar{H}|D)} = \frac{P(D|H)P(H)}{P(D|\bar{H})P(\bar{H})}$$
What we have here is the formula for computing the posterior odds for \(H\). Odds express our uncertainty in terms of how many times more likely \(P(H|D)\) is than \(P(\bar{H}|D)\). And because \(P(H|D) + P(\bar{H}|D) = 1\) we can eventually get back to $$P(H|D)$$ from our odds (this is not true if we compare two hypotheses that are not complements of each other). The trick when we learn our model is that we actually have examples of \(\bar{H}\).
Since we're no longer talking about probabilities, we're dealing with odds, let's call \(\frac{P(H|D)}{P(\bar{H}|D)}\), just \(O(H|D)\), or the odds of our hypothesis give our data. Likewise we can clean up our formula a bit. We can just rename \(\frac{P(H)}{P(\bar{H})}\) our prior odds, \(O(H)\), and now we have a much cleaner formula defined in terms of odds and our likelihood ratio.
$$O(H|D) = \frac{P(D|H)}{P(D|\bar{H})}O(H)$$
Not a bad start at solving our problem. Next we need a way to learn the right side of this equation from our data.
Finding a linear model.
The simplest, and often most useful, model to use is often a linear model:
$$y = \beta x+ \beta_0$$
This just means that y increase or decreases at some constraint rate(s) \(\beta\) with some intercept(s) \(Beta_0\). This is a simple way to look at things but if we have data we can learn the optimal parameter for this with linear regression. Unfortunately our current probabilistic solution to the coffee problem doesn't look anything like this... yet.
Log transformation to the rescue.
You'll notice that the odds form of our probability problem has only multiplication and division in it which makes it seem like we're a bit a ways off from a nice linear solution. But there's a very useful trick we can perform to get this in the right form: we can simply log transform it! We'll use \(log_{10}\) for now since it tends to be easier to make intuitions about things in base 10.
$$log_{10}(O(H|D)) = log_{10}(\frac{P(D|H)}{P(D|\bar{H})}O(H)) = log_{10}(\frac{P(D|H)}{P(D|\bar{H})}) + log_{10}(O(H))$$
It's a bit messy, but if we look we now have a linear equation! Notice that \(O(H)\) does not depend at all on our data vector, just like in the linear model \(\beta_0\) is just a constant and does not depend on \(X\). So for our linear model we can just say that:
$$\beta_0 = log_{10}(O(H))$$
Or that \(\beta_0\) is the log of the prior odds. We'll explore this very useful property of logistic regression more in the next post.
Now we come to the heart of our model. We're going to just go ahead make the simplifying assumption that, ignoring our prior, the log likelihood ratio is simply a linear function of \(D\). So for example, perhaps that a decrease in temperature of our water causes the log likelihood to decrease linearly. This turns out to be a great property because if we increase the probability of something from 0.01 to 0.1 is not a linear increase of 0.09 in the probability, but an exponential increase! So if we want to model probabilities in a linear fashion, we're going to want to think in terms of log transformed data.
If we make this assumption we can model the likelihood ratio as \(\beta D\). And now we have a beautifully linear solution to our problem. Here we'll reference log odds as \(lo\):
$$lo(H|D) = \beta D + \beta_0$$
With this linear form we can learn the likelihood ratio and prior odds, in log form, as a linear function of the data. This is what makes logistic regression a linear model, at its heart we are assuming that the likelihood, \(P(D|H)\), ultimately has a linear relationship with its inputs. But in order to see this linear relationship we needed to transform our output into log odds.
Where we are so far: probabilities, odds and log odds.
Let's recap a bit to make sure we know what's happened so far. We started wanting to know \(P(H|D)\), the probability take our cup of coffee would be great given our brewing setup, which is out data \(D\). With Bayes' theorem alone we could almost solve this problem except that we couldn't figure out a way to compute \(P(D)\). This means that rather than looking at just the probability of \(P(H|D)\) we needed to look at the odds, \(O(H|D)\) which compares the probability that the coffee is great with the probability that it's not, \(\bar{H}\). Odds will give us results in terms of ratios of how likely one hypothesis is to the other:
\(O(H|D)= 10\) means the coffee is tens times as likely to be good as it is to not be.
\(O(H|D)= \frac{1}{10}\) means the coffee is ten times as likely to not be good.
Notice that the odds format is asymmetrical in that as evidence grows for our hypothesis the result grows towards infinity and as evidence grows against our hypothesis the odds shrinks to 0.
When we transformed our odds to the \(log_{10} O(H|D) \) odds we fix this asymmetry:
\(log_{10} O(H|D) = 1\) means that great coffee is 10 times more likely
\(log_{10} O(H|D) = 2 \) means that great coffee is 100 times more likely
\(log_{10} O(H|D) = -1\) means that great coffee is 10 times less likely
\(log_{10} O(H|D) = -2\) means that great coffee is 100 times less likely
So aside from giving us a nice linear way to look at our problem, framing our problem in log odds actually makes a lot of sense when we try to interpret the results!
The trouble with learning our model
We have a nice linear format for our problem that looks basically just like linear regression which is.
$$y=\beta x + \beta_0$$
It seems only natural that we should be done now and can solve our problem by minimizing least squares like we would any other linear regression problem. In this approach we don't need to transform our data since we are just using \(D\) as it is and assuming the log odds increase or decrease based on the values of our data. But we do need to think about how we're going to transform our target variable. For the target \(y\) that we want to train on we already have data in the \(P(H|D)\) form. For the cases that are successful we know that \(P(H|D) = 1\) and that for the cases that are unsuccessful \(P(H|D) = 0\). In order to train our linear model we need to transform our target data into log odds form first.
But there is annoying problem here! To transform a probability into odds we can follow this simple rule:
$$O(H) = \frac{P(H)}{1-P(H)}$$
But we can see there's a bit of a problem, because our probabilities are absolute 1s or 0s. The odds for the positive cases are \(\frac{1}{0}\) which is undefined! And even if we could solve this problem when we want to take the \(log_10\) of our odds for the negative case we can't because those will be \(\frac{0}{1}\), and \(log_{10} 0\) is also undefined!
Turning our log odds back into probabilities: the inverse logit!
We're frustratingly close to our solution, and even though we can't quite get there yet, we've learned something valuable. At the heart of our probability problem is a linear model. We can't transform our target variable, but if we can transform this linear model itself model back into a probability then we will have our solution!
It turns out that this is surprisingly easy! We just have to undo everything we've done, but this time do it to the linear model. Our model is currently written in terms of log odds so the first thing we have to do is undo our log transformation. We can do this just by taking 10 to the power of our linear equation:
$$O(H|D) = 10^{(\beta D + \beta)}$$
That was pretty easy! Now we just have to turn our odds into probabilities, which is just as easy as turning probabilities into odds. We can use this rule:
$$P(X) = \frac{O(X)}{1+O(X)}$$
If we do this we can see that:
$$P(H|D) = \frac{10^{(\beta D + \beta)}}{1 + 10^{(\beta D + \beta)}}$$
Since we couldn't transform our target values, we've had to transform our \(\beta D +\beta_0\), but that's okay because it has the same effect either way, and this time we can handle the fact that our outcomes are absolute 1s and 0s.
There are still two more simplifications we can make just to make this prettier and more mathematically acceptable. First, no serious mathematicians use \(log_{10}\), \(ln\) is much better so we need to swap out that 10 for an \(e\). We're not doing anything specifically related to keeping our results in base 10 so there's no problem at all with this change, the effects will be the same.
$$P(H|D) = \frac{e^{(\beta D + \beta_0)}}{1 + e^{(\beta D + \beta_0)}}$$
And it also turns out, quite conveniently that:
$$\frac{e^x}{1+e^x} = \frac{1}{1+e^{-x}}$$
Which means that we can transform our final equation to be that mysterious formula we saw at the beginning:
$$P(H|D) = \frac{1}{1+e^{-(\beta D + \beta_0)}}$$
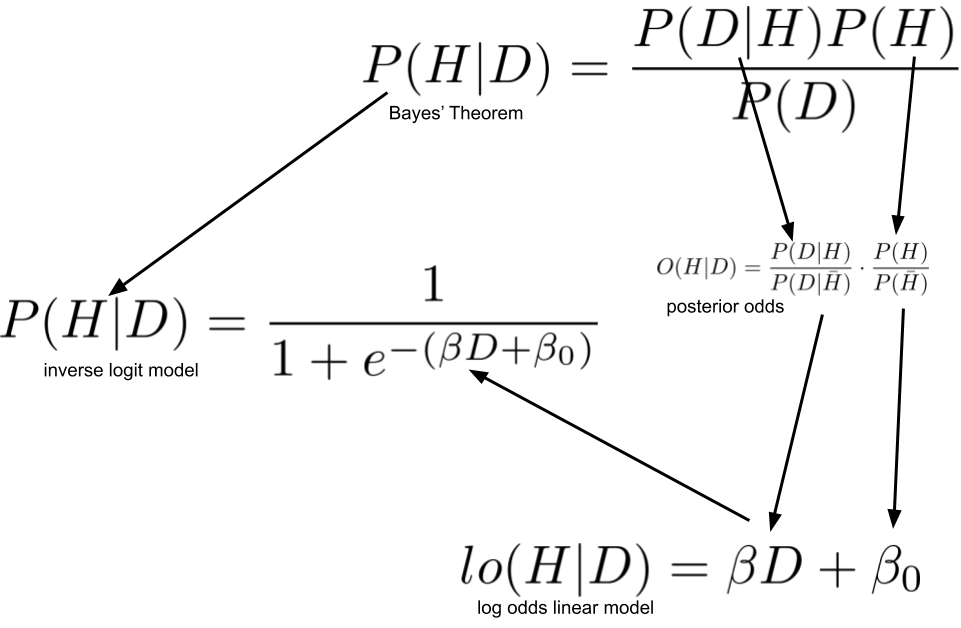
Here we see that this formula is simply a way to transform our log odds back into a probability! Which is, of course, literally what the "inverse logit" means, "logit" being the "log odds" function. The logit function takes probabilities and transforms them into log odds, the inverse logit takes log odds and turns them into probabilities! The following image should help visualize what we've done in this post.
This diagram show how we transformed Bayes’ Theorem into Logistic Regression
One of the central insights we get from deriving logistic regression is to see very clearly how logistic regression is a linear model. We initially model our problem as Bayes' theorem, but we don't know the likelihood for the data given our hypothesis and prior probability for our hypothesis. We want to be able to learn these from the data, and to do that we ultimately make the simplifying assumption that there is a linear relationship between the log odds of our hypothesis and our data \(D\). In the next post we'll see that we can make further use of this knowledge by adjusting our prior probability after the model has been trained!
Having walked through all of this you can rebuild this anytime you need starting from the basics of Bayes' Theorem and linear regression. We can now train a model to learn \(\beta\) and \(beta_0\) using the inverse logit. Of course now that we've transformed our function we can't necessarily use least squares as our, but the topic of how we choose a loss function for this model will have to be the subject of the third post in this series.
Conclusion
While this is a pretty convoluted way to make a cup of coffee, learning about the relationship between Bayes' Theorem and Logistic regression provides us with some pretty powerful insights into the way logistic regression really works.
We've also gotten a little taste of the power of the generalized linear model. A major part of what we did here was find some function, in this case the inverse logit, that can transform a linear model. With a bit of refinement we can see how this can be extended to perform a variety of other regressions based on other transformations of the linear model.
This post is going to be part in a series on logistic regression. In the next post we'll be looking at prior probability and logistic regression. In that post we'll see how you can update prior probabilities assumed by your model after you have trained your model, which is very useful anytime you train your model using a different distribution of data than the model will be predicting on.
If you enjoyed this post please subscribe to keep up to date and follow @willkurt!
If you want to learn more about Bayesian Statistics and probability: Order your copy of Bayesian Statistics the Fun Way No Starch Press!
If you enjoyed this writing and also like programming languages, you might enjoy my book Get Programming With Haskell from Manning.